【摘要】数形结合作为初中数学教学的一种重要手段，贯穿初中数学教育始终，有利于培养学生创新意识，使学生养成灵活的数学思维方式，激发学生自主学习的热情。本文将分析数形结合在初中数学教学中的重要作用，探讨如何在数学教学中运用数形结合的思想。

【关键词】数形结合；初中数学；运用；教学

随着教育改革的深入，对学生的考察不再局限于课本教材知识，还在于是否能够熟练运用知识。为此，教师需要转变教学方式，改变单一的教学方法。数形结合思想能够加深学生对数学知识的理解，提高课堂教学效率，是数学教学中的一种有效手段[1]。

一、数形结合在初中数学教学中的重要性

数形结合是一种重视直观感知的教学方法，通过板书、多媒体等媒介将繁杂的数学理论知识转化成图形，经过代数与图形相结合，抽象的数量关系、数学语言就能被转化为形象直观的几何图形[2]。在当前的初中数学教学中，数形结合思想被广泛应用。为了使学生的注意力得到提高和集中，教师将数形结合思想融入教学之中，使问题一目了然。将数形结合思想引入教学中，能使枯燥的数学知识变得形象有趣，激发学生学习的积极性，同时也能提高学生的数学分析能力。因此，数形结合思想在初中数学教学中具有独特的作用。它能够将几何知识，如圆形、多边形、数轴等，同代数知识如方程、函数、不等式等相联系，锻炼学生在数学学习中的灵活性和敏捷性。

二、数形结合思想的应用策略

1.数形结合思想在初中数学教学中的引入

在对没有接触过数形结合概念的初中学生进行教学时，教师需要在授课过程中自然地将数形结合思想融入知识点，才能使数形结合思想发挥出事半功倍的效果[3]。例如，教师可以使用数轴来让学生理解绝对值的概念，通过将正数、负数和零与它们在数轴上的位置相对应，使学生能够形象直观地理解绝对值概念，为往后的学习打好基础；又如，函数是数学教学中的一个难点，教师可以利用对应的函数图像，来让学生直观地掌握其特点和主要参数，理解变量和变量之间的关系，达到融会贯通、举一反三的目的。这样，教师在讲解数学概念过程中自然地引入数形结合的思想，就能大大提高教学效率。

2.数形结合思想的具体实施

运用数形结合思想解答初中数学问题，主要有两种方式，一是利用代数描述图形，将几何问题代数化。将图形性质赋予数量意义，用代数来描述图形，寻找能够表达问题的数量关系式，就能很好地用“数”来解决“形”的问题。二是利用图形展示代数，将相对应的图形意义赋予抽象的数量关系式，就会使数量关系式的理解变得直观、形象。熟练运用数与形之间的转化，就能更好地掌握解题关键，轻松解决数学难题。

2.1利用代数描述图形

数轴能够表示实数，实数与数轴上的点相对应，要形象、直观地理解实数，可以将数与数在数轴上的对应位置相联系，寻找它们之间的关系。

案例1 已知图1的△ABO中，A的坐标为（3,4），B的坐标为（6,3），求△ABO的面积。

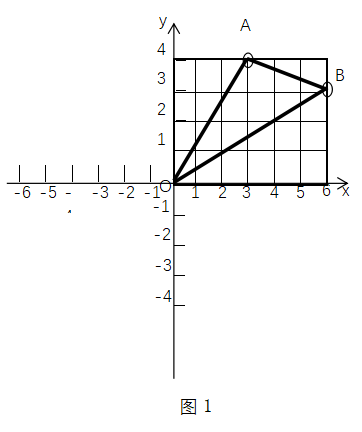
解析：该题主要考察运用坐标解决图形面积。学生在尚未学习到勾股定理的情况下，无法通过求出某一条边的长度以及这条边上的高来求出面积，则可以过点A作y轴的垂线，垂足为M，过B作x轴的垂线，垂足为N，两条垂线交于点Q，可得长方形OMQN。求出OMQN的面积，再求出△AOM、△ABQ、△BNO的面积，用长方形的面积减去三个三角形的面积，即可得出△ABO的面积。

解答：如图2所示，过点A作y轴的垂线，垂足为M，过点B作x轴的垂线，垂足为N，两垂线交点为Q，可得长方形OMQN的面积

S长方形OMQN=6×4=24。△AOM的面积为S△AOM=3×4×0.5=6，△ABQ的面积为

S△ABQ=1×3×0.5=1.5，△BNO的面积为S△BNO=3×6×0.5=9。

所以△ABO的面积S△ABO=S长方形OMQN ‐S△AOM ‐S△ABQ  ‐S△BNO=24-6-1.5-9=7.5。

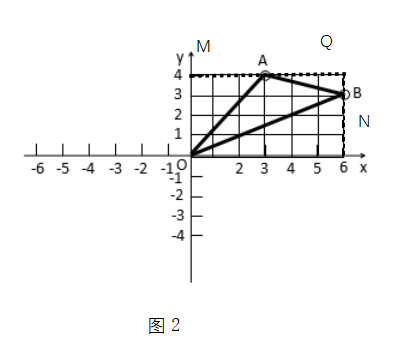
这样，通过将实数与其在数轴上的位置相对应，便可得出三角形的面积。

2.2利用图形展示代数

除了可以使用数轴来表示实数与数轴之间的关系，还可以用数轴来解决绝对值的问题。

案例2 已知A＜0，B＞0，且＜，那么A+B等于（ ）。

   A. 负数     B. 正数    C. 零   D.无法确定

解析：直接在数轴上表示这两个点，既直白、又简便，很快得出该题的答案为B。如图3所示。

如此，利用图形来表示代数，便能化简复杂的数学关系，使答案一目了然。

三、结束语

综上所述，将数形结合思想融入数学教学之中，能够将错综复杂的问题转变得直观简便，使解题思路一目了然，另外，能够在一定程度上激发学生的学习积极性。以初中数学教材为基础，在数学概念的讲解、习题的分析巩固中深入浅出地引入数形结合思想，引导学生学会灵活使用数形结合思想来解决问题，就能促使学生的立体几何分析能力得到提高，有利于启发学生数学思维，提高数学教学质量与教学效率。

【参考文献】

[1]王爱花. 初中数学数形结合思想教学研究与案例分析[J]. 中国校外教育, 2017(5):64-64.

[2]伍斌. 初中数学数形结合思想教学研究与案例分析[J]. 中国校外教育, 2017(11):60-60.

[3]胡萍. 初中数学数形结合思想教学研究与案例分析[J]. 求知导刊, 2016(20):86-86.